Primordial Construct: Mathematics

Negative «	Zero Δ	Positive »
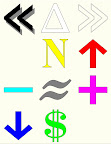
	N	Sum ∑ ↑
Subtract –	Identity ≈	Add +
↓	$

Negative «	Zero Δ	Positive »
	N	Product ∏ ↑
Divide ÷ –	Identity ≈	Multiply × +
↓	$

Subtraction and division are not commutative, i.e. the order of the operands cannot be interchanged; but addition and multiplication are commutative, i.e. the operands are interchangeable. Sum and Product are group operations.

a – b ≠ b – a, unless a = b

a ÷ b ≠ b ÷ a, unless a = b

a + b = b + a

a × b = b × a

Negative «	Zero Δ	Positive »
	Imaginary N	Exponential ↑
Rational –	Identity ≈	Irrational +
Reciprocal ↓	Real $

A numerical anomaly exists in the realm of numbers. Square any real number and the result is always positive. For example:

2² = 2 × 2 = 4 and
(–2)² = –2 × –2 = 4.

Square roots operate in a complimentary fashion. Reversing the above example, the square root of 4 is either 2 or –2. But what is the square root of a negative number? It can be represented as the square root of a positive number, straight forward for positive real numbers, times the square root of negative one. But the square root of negative one violates the standard convention for real numbers. The square root of negative one is the numerical anomaly. The symbol for the square root of negative one is i, for imaginary, i.e. √–1 = i and i² = –1.

Given x² + 1 = 0, then x = √–1 = i or –i.
Given x² + 4 = 0, then x = √–4 = 2i or –2i.

Rational numbers can be expressed as an integer or a fraction.

Irrational numbers have no explicit integer or fraction representation. Any decimal equivalent requires an infinite number of digits. Symbolic representations are needed to express irrational numbers. Examples are: π and √2

A hindsight perspective sees the future as an extension of the past. Momentum represents the single greatest predictor of things to come.

A foresight perspective realizes that only now exists. The future is what we make it, while acting in the present.